Application of the law of Zipf-Mandelbrot to the diagnosis of normal and acute cardiac dynamics

Abstract
Background: The capacity of statistical fractals in the evaluation of the complexity of different systems whose dynamics can be evaluated from the frequencies of a variable is known. This is why the measure of the statistical fractal dimension is used, which can be calculated with the Zipf-Mandelbrot law, this mathematical law has been applied in cardiology evaluating the degree of complexity of cardiac dynamics. In the present work, the Zipf-Mandelbrot law was applied together with the diagnostic methodology previously developed to evaluate normal cardiac dynamics and acute disease. Material and methods: 15 Holter records were taken; 10 with normal diagnosis and 5 with acute pathologies of patients of the Intensive Care Unit. The frequencies of occurrence of the heart frequencies of each dynamics were organized hierarchically in ranges of 15 lat/min, in search of the hyperbolic behavior required for the application of the law of Zipf-Mandelbrot. Subsequently, a linearization was performed and the statistical fractal dimension was obtained for each dynamics. Results: The values of the statistical fractal dimension for acute cardiac dynamics varied between 0.4925 and 0.6061, whereas for normal dynamics they varied between 0.7134 and 0.9749, evidencing the differentiation between both groups. Conclusions: The statistical fractal behavior of the cardiac dynamics was corroborated, as well as the loss of complexity for the acute dynamics with respect to the normal dynamics.

Key words
acute heart disease

Artículo completo
Introducción

La caracterización de los objetos regulares fue cuestionada a partir de los resultados de los estudios de sir Fray Richardson, cuestionamiento que planteó Benoit Mandelbrot,¹ quien desarrolló la geometría fractal, mediante la cual se pueden caracterizar objetos irregulares, denominados fractales, por medio de la dimensión fractal. Existen diferentes tipos de fractales, uno de estos son los fractales estadísticos que corresponden a sistemas que pueden ser caracterizados a partir de la distribución de las frecuencias de aparición de determinadas variables que se presentan de manera jerárquica. La ley de Zipf-Mandelbrot^2-5 se utiliza para el cálculo de la dimensión de los fractales estadísticos, la cual caracteriza el grado de complejidad de dichos fractales. Esta medida ha permitido medir la pérdida de la complejidad de textos escritos por pacientes con enfermedad de Alzheimer.⁶

De acuerdo con la Organización Mundial de la Salud (OMS), las enfermedades cardiovasculares (ECV) siguen siendo la principal causa de mortalidad a nivel mundial;⁷ llegándose a reportar cuatro millones de muertes al año⁸ por esta causa en Europa; en algunos países de ese continente la cifra llega a ser incluso más de dos veces la obtenida por todos los tipos de cáncer. La tasa de muertes atribuidas a las ECV en los Estados Unidos durante 2011 fue de 229.6 por 100 000 personas,⁹ cada 40 segundos fallece un estadounidense a causa de una ECV, también se ha informado que las tasas de mortalidad por enfermedad coronaria han aumentado en los EE.UU. y en muchos países europeos.¹⁰

En la literatura médica cardiológica, la variabilidad de la frecuencia cardíaca (VFC) es considerada un buen indicador pronóstico de pacientes con dinámicas cardíacas agudas,¹¹ sin embargo, sus variaciones también se encuentran asociadas con un número considerable de enfermedades cardiovasculares.^12,13 Otras investigaciones han mostrado que el sistema cardiovascular presenta un comportamiento no lineal, observando en muchos casos conductas caóticas,¹⁴ que pueden ser caracterizadas a partir de la geometría fractal, mediante la cual también se pueden evaluar diferentes estructuras del cuerpo humano.^15,16

A partir de los trabajos de Goldberger y colaboradores sobre los cambios espectrales abruptos y las oscilaciones de baja frecuencia sostenidas en pacientes con alto riesgo de muerte súbita cardíaca, se encontró que se puede asociar la pérdida de la complejidad y la reducción de la dinámica de la respuesta cardíaca antes de la muerte súbita y el envejecimiento.^17,18 Para evaluar la complejidad de la dinámica cardiovascular se utilizó la entropía aproximada,¹⁹ análisis multifractales para analizar la complejidad y el comportamiento de la VFC, en diferentes situaciones como por ejemplo, la evaluación de la dinámica cardíaca de pacientes antes y después de ser sometidos a una revascularización miocárdica.²⁰ En esta investigación se encontró que este tipo de análisis permite evaluar la recuperación del paciente durante las primeras semanas después de la cirugía.²¹ En cambio, estudios recientes han encontrado el surgimiento de la complejidad relacionada con la VFC a partir del análisis de la entropía multiescala.²² Sin embargo, se encuentran estudios que subrayan la necesidad de hacer más específicos los análisis hechos con base en la no linealidad de las dinámicas temporales.²³

Desde la aplicación de la física y la matemática se han desarrollado nuevos estudios que simplifican en una sola metodología el análisis de la dinámica cardíaca fetal,^24,25 del adulto^26,27 y neonatal.²⁸ La confirmación clínica de estas metodologías ha sido mostrada a partir de su análisis en arritmias cardiacas,^29,30 así como en un número mayor de casos,^31,32 permitiendo también evaluar efectivamente dinámicas cardiacas de pacientes que se encuentran en la Unidad de Cuidados Intensivos (UCI).³³ Su aplicación clínica se debe a que mediante cada una de ellas se puede diferenciar la dinámica cardíaca normal del enfermo, así como su evolución a estados de agudización, dejando de lado análisis rigurosos que requieran la aplicación de otros métodos para comprender los resultados hallados mediantes estas metodologías.

Recientemente, se realizó un estudio en el cual se aplicó la ley de Zipf-Mandelbrot para desarrollar una metodología de ayuda diagnóstica, que permitió evaluar el grado de complejidad de la dinámica cardíaca normal y aguda. El estudio reveló, a partir de las dimensiones fractales estadísticas, que la dinámica cardíaca normal se caracteriza por presentar una mayor complejidad respecto de la dinámica cardíaca aguda, diferenciando de manera cuantitativa el grado de agudización de la dinámica cardíaca.³⁴ El propósito de esta investigación es aplicar la metodología fundamentada en la ley de Zipf-Mandelbrot a 15 registros de la dinámica cardíaca, cinco de ellos de pacientes de la UCI.


Metodología
Dimensión fractal estadística

Se halló calculando el inverso multiplicativo negativo de la pendiente de la linealización logarítmica del comportamiento hiperbólico de las frecuencias de aparición de los rangos de frecuencias cardíacas respecto de los rangos definidos por la ley de Zipf-Mandelbrot. Se expresa mediante la ecuación:





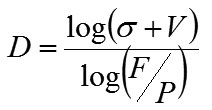
siendo, D: la dimensión fractal; s corresponde al rango asumido para cada frecuencia, P es la frecuencia de aparición de la frecuencia cardíaca, V está definida por V=1/N-1 donde N es el número de frecuencias medidas; por último, F corresponde a un cofactor secundario en el proceso de linealización, el cual fue realizado aplicando el método de cuadrados mínimos.


Procedimiento

Para la realización de este estudio se tomaron 15 registros Holter de pacientes mayores de 21 años, provenientes de las bases de datos del grupo Insight, los cuales contaban con un tiempo mínimo de 21 horas de registro. Se incluyeron dos grupos; el primero, de diez registros, con diagnóstico clínico entre los límites de normalidad, y el segundo, de cinco registros, con pacientes con diagnóstico de enfermedad aguda de la Unidad de Cuidados Intensivos (UCI) de la Clínica del Country. Estos registros fueron evaluados y diagnosticados por un electrofisiólogo experto de acuerdo con los parámetros convencionales.

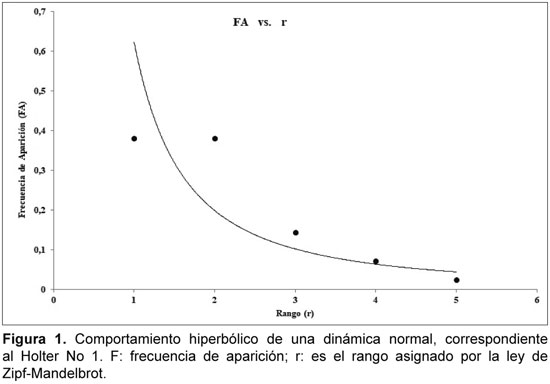
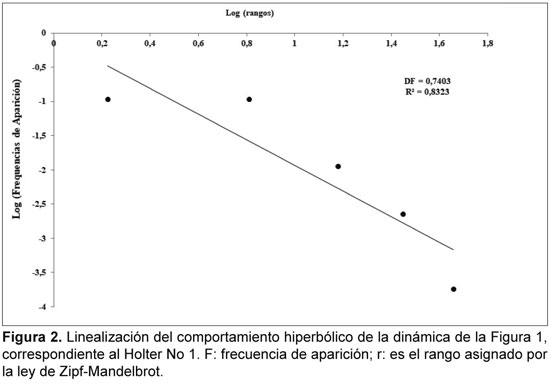
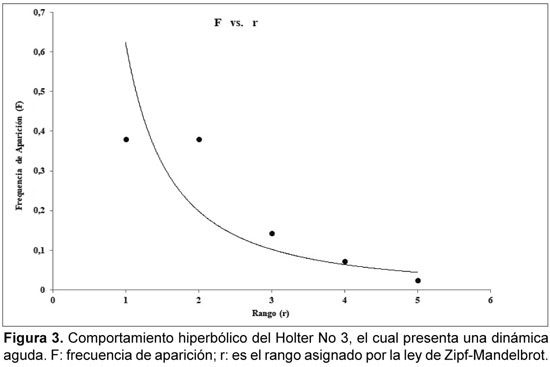
De cada Holter se tomó el valor de la frecuencia cardíaca máxima y mínima durante cada hora. Seguidamente, se realizó un conteo del número de frecuencias cardíacas que se encuentran en cada rango de 15 lat/min, se calculó la frecuencia de aparición de los rangos de 15 lat/min y se aplicó la ley Zipf-Mandelbrot a estos valores. Para ello, las frecuencias de aparición de los rangos fueron ordenadas de mayor a menor, asignando a cada una un número entero, empezando por 1 y aumentando en una unidad para las siguientes frecuencias de aparición ordenadas jerárquicamente. Estos datos fueron graficados para confirmar el comportamiento hiperbólico necesario para la aplicación de la ley (Figuras 1 y 3). A esta gráfica se le aplicó una linealización logarítmica (Figuras 2 y 4), hallando así la dimensión fractal estadística para cada dinámica.


















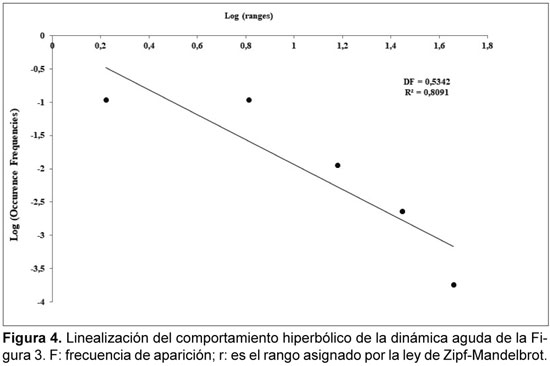
Posteriormente se analizaron estos valores para ver si se encontraban en el rango consistente de la ley, el cual puede presentar cualquier valor real entre 0 y 1. Finalmente, se aplicaron los parámetros diferenciadores entre normalidad y enfermedad aguda hallados previamente.³⁴


Aspectos éticos

El presente estudio cumple con los principios éticos de la Declaración de Helsinki de la Asociación Médica Mundial y, según la Resolución 8430 de 1993 del Ministerio de Salud colombiano, según la cual esta investigación es declarada como una investigación con riesgo mínimo dado que se realizan cálculos físicos y matemáticos sobre reportes de exámenes y paraclínicos no invasivos, que han sido prescritos previamente según protocolos establecidos convencionalmente, protegiendo también, el anonimato e integridad de los participantes.


Resultados

La dimensión fractal estadística para los registros Holter normales varió entre 0.7134 y 0.9749, y para los registros con enfermedad aguda entre 0.4925 y 0.6061 (Tabla 1), mostrando que las distribuciones de rangos de frecuencias cardíacas de las dinámicas patológicas son menos complejas que las dinámicas normales (Figuras 1 y 3). Las linealizaciones obtenidas para hallar las dimensiones fractales tuvieron valores del factor de correlación, R², entre 0.7560 y 0.9876 para normalidad, y entre 0.8091 y 0.9938 para enfermedad aguda, evidenciando el comportamiento a escala de la dinámica cardíaca (Figuras 2 y 4). Todas las dimensiones fractales estuvieron en los rangos establecidos,³⁴ a excepción de una que corresponde a una dinámica normal, que presentó un valor mayor al límite superior del rango establecido para las dinámicas cardíacas normales.






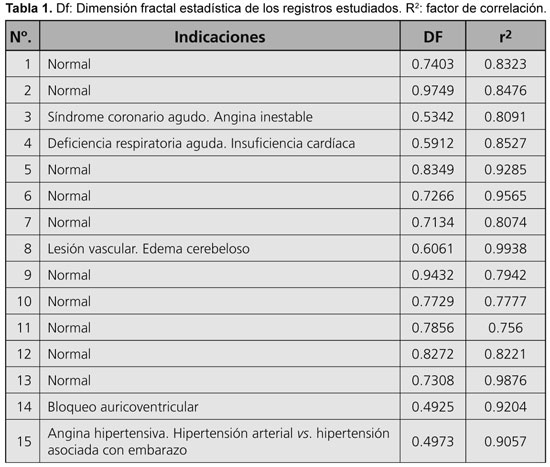
Discusión

Este es el primer trabajo en el cual se muestra la aplicabilidad de la metodología de ayuda diagnóstica fundamentada en la ley de Zipf-Mandelbrot, evaluando 15 dinámicas cardíacas, las cuales incluyen dinámicas cardíacas normales y con enfermedad aguda de pacientes de la UCI. El análisis del ordenamiento jerárquico de las frecuencias cardíacas máximas y mínimas cada hora para rangos de 15 lat/min, permitió hallar un comportamiento hiperbólico para las frecuencias cardíacas, revelando una autorganización fractal de la dinámica cardíaca de pacientes con patologías agudas y para casos dentro de límites normales, según diagnóstico clínico convencional, indicando que a medida que los grados de complejidad descienden, aumenta el grado de agudización de los pacientes.

Previamente se estableció que los mayores grados de complejidad de la dinámica cardíaca son característicos de las dinámicas cardíacas normales, mientras que las dinámicas cardíacas con enfermedad aguda presentan complejidades de menor valor, mostrando de manera más sencilla los valores matemáticos que caracterizan el grado de complejidad de la dinámica cardíaca a medida que esta agudiza,³⁴ lo que fue confirmado en el presente estudio. De acuerdo con los resultados, la evolución entre normalidad y enfermedad aguda quedaría matemáticamente acotada presentando valores de dimensión fractal estadística entre el límite superior de enfermedad aguda y el límite inferior de normalidad. Desde esta perspectiva físico-matemática se han desarrollado otros trabajos, logrando diagnósticos de aplicabilidad clínica al diferenciar normalidad, enfermedad crónica y enfermedad aguda, así como la evolución entre estos estados, a partir de las proporciones de la entropía.³² Del mismo modo, se desarrolló una ley exponencial que permite calcular la totalidad de posibles dinámicas cardíacas posibles, diferenciando cuantitativamente normalidad, enfermedad aguda y evolución entre ellos,^29,31 lo cual simplifica otros métodos de evaluación desarrollados con este mismo fin.^21-23 Siguiendo esta perspectiva, esta nueva metodología constituye una nueva forma cuantitativa, objetiva y reproducible de evaluar el grado de complejidad de la dinámica cardíaca, aplicable tanto a pacientes ambulatorios como pacientes de la UCI con diagnóstico de infarto agudo de miocardio (IAM) o con agudización de la dinámica cardíaca.

Previamente, Rodríguez y colaboradores^35,36 evaluaron la dinámica cardíaca a partir de las leyes de la probabilidad, y encontraron un diagnóstico matemático que requería analizar 26 rangos de frecuencias cardíacas, e incluía la evaluación de tres parámetros y otros subparámetros para establecer el estado de normalidad, enfermedad o evolución. Un estudio de la capacidad diagnóstica de esta metodología halló valores de sensibilidad del 100% y especificidad del 73.3%.³⁵ El presente método tiene una mayor simplicidad, pues se necesita sólo un valor numérico -el grado de complejidad de la dinámica cardíaca- para establecer el estado de normalidad/enfermedad, evitando de esta manera el análisis de la dinámica cardíaca mediante más parámetros.

Desde la teoría de los sistemas dinámicos, Goldberger y colaboradores¹⁵ desarrollaron una nueva concepción normalidad/enfermedad, donde hallaron que la enfermedad se caracteriza por presentar estados altamente regulares o irregulares, mientras que la normalidad se halla en medio de estos dos extremos, contradiciendo la noción de homeostasis; sin embargo, esta concepción no cuenta con valores característicos de normalidad y enfermedad de aplicabilidad diagnóstica. En contraposición, la presente metodología logra cuantificar, a partir de la dimensión fractal estadística, las diferencias entre dinámicas normales y agudas, proporcionando una cuantificación objetiva y reproducible de aplicabilidad diagnóstica, donde la disminución de los valores de dimensión fractal se asocia con enfermedad aguda.

En el contexto de los sistemas dinámicos, Huikuri y colegas³⁷ caracterizaron la dinámica cardíaca de pacientes posinfartados y con FE menor del 35%, encontrando índices predictores de mortalidad que superan los convencionales. Sin embargo, las implicaciones que tiene la aplicación de este y otros trabajos desarrollados desde esta línea aún se encuentra en discusión.³⁸ En cambio, en el presente estudio se estableció un orden matemático que permite la evaluación de dinámicas cardíacas con IAM de manera independiente, sin que la metodología se vea afectada por factores causales, poblaciones y por tratamientos terapéuticos.

El desarrollo de metodologías fundamentadas en la ley de Zipf-Mandelbrot ha permitido la caracterización objetiva de diferentes fenómenos en medicina. Entre ellas, se encuentra la diferenciación en los grados de complejidad del repertorio T específico contra el alérgeno poa P9 en un paciente alérgico en presencia y ausencia de interferón a, y en los clones de células Th.³⁹ En el área de la ginecología, se desarrolló una nueva metodología diagnóstica de la monitoría fetal con base en el análisis de la aparición de los componentes dinámicos del sistema (CDS) mediante la ley de Zipf-Mandelbrot,^25,40 estableciendo diferencias cuantitativas del comportamiento normal y anormal de una dinámica cardíaca fetal, evitando los problemas de reproducibilidad interobservador e intraobservador del método convencional.⁴¹

Continuando con esta nueva perspectiva de investigación, la aplicación de otras teorías físicas y matemáticas a diferentes sistemas ha contribuido al desarrollo de nuevas metodologías predictivas en otras áreas, como la predicción de alteraciones cardíacas asociadas con sepsis neonatal,²⁸ o el desarrollo una metodología que permite predecir el recuento de linfocitos TCD4 de pacientes con infección por VIH.³⁷ Del mismo modo se han obtenido predicciones en inmunología,⁴² en biología molecular⁴³ y en la dinámica de epidemias tales como la de malaria en Colombia.⁴⁴ También se logró una generalización de la totalidad de arterias coronarias normales y restenosadas de utilidad para modelos experimentales,⁴⁵ y un diagnóstico de células preneoplásicas y neoplásicas de cérvix,⁴⁶ trabajos de utilidad tanto a nivel clínico como experimental y en el campo de la salud pública.

Agradecimientos

Este artículo es producto del proyecto: Evaluación física y matemática de variables hemodinámicas de pacientes de la Unidad de Cuidados Intensivos fundamentada en la geometría fractal y los sistemas dinámicos: Cuantificaciones de aplicación clínica en 14 horas; desarrollado en el Centro de Investigaciones de Clínica del Country, en alianza con la Universidad Militar Nueva Granada.

Agradecemos a la Universidad Militar Nueva Granada por su apoyo a nuestras investigaciones. Especialmente a la Vicerrectoría de Investigaciones y la Facultad de Medicina. Extendemos un agradecimiento especial a la Dra. Nydia Alexandra Rojas, Directora de Investigaciones de la Facultad de Medicina, al Dr. Jorge Luque, Decano de la Facultad de Medicina y a la Dra. Yanneth Méndez, Vicerrectora académica.

Agradecemos también al Centro de Investigaciones de la Clínica del Country, en especial a los doctores Tito Tulio Roa, Director de Educación Médica; Jorge Ospina, Director Médico, y Alfonso Correa, Director del Centro de Investigaciones; a la Doctora del Centro Adriana Lizbeth Ortiz, epidemióloga, las enfermeras Silvia Ortiz y Sandra Rodríguez, por el apoyo a nuestras investigaciones.

Bibliografía del artículo
1. Mandelbrot B. Scaling and power laws without geometry. In: The Fractal Geometry of Nature. Freeman Ed. San Francisco, pp. 344-8, 1972.
2. Zipf GK. The human behavior and the principle of least effort. Addison-Wesley Press, Cambridge, MA, 1949.
3. Mandelbrot B. Information theory and psycholinguistics: a theory of words frequencies, in: Lazafeld P, Henry N. (Eds.) Readings in mathematical social science, MIT Press, Cambridge, MA, 1966.
4. Mandelbrot B. Structure formelle des textes et comunication. World. 10:1-27, 1954.
5. Corral Á, Boleda G, Ferrer-i-Cancho R. Zipf's law for word frequencies: Word forms versus lemmas in long texts. PloS one, 10(7), e0129031, 2015.
6. Hernández A, Diéguez F. La ley de Zipf y la detección de la evolución verbal en la enfermedad de Alzheimer. Anuario de Psicología 43(1):67-82, 2013.
7. WHO. The atlas of heart disease and stroke. Deaths from coronary heart disease. Disponible en: http://www.who.int/cardiovascular_diseases/en/cvd_atlas_14_deathHD.pdf?ua=1.
8. Nichols M, Townsend N, Scarborough P, Rayner M. Cardiovascular disease in Europe 2014: epidemiological update. European Heart Journal 35(42):2950-2959, 2014. doi: 10.1093/eurheartj/ehu299.
9. Mozaffarian D, Benjamin E, Go AS, Arnett DK, Blaha MJ, et al. Heart disease and stroke statistics. Update. A report from the American Heart Association. Circulation 131:e29-e322, 2015.
10. OMS. Centro de prensa. Enfermedades cardiovasculares. Disponible en: http://www.who.int/mediacentre/factsheets/fs317/es/.
11. Harris P, Stein PK, Fung GL, Drew BJ. Heart rate variability measured early in patients with evolving acute coronary syndrome and 1-year outcomes of rehospitalization and mortality. Vasc Health Risk Manag 10:451, 2014.
12. Shahbazi F, Asl BM. Generalized discriminant analysis for congestive heart failure risk assessment based on long-term heart rate variability. Comput Methods Programs Biomed pii: S0169-2607(15)00217-5, 20105. doi: 10.1016/j.cmpb.2015.08.007.
13. Lakusic N, Mahovic D, Kruzliak P, Cerkez Habek J, Novak M, Cerovec D. Changes in heart rate variability after coronary artery bypass grafting and clinical importance of these findings. Biomed Res Int. 2015;2015:680515. doi: 10.1155/2015/680515. Epub 2015 May 20.
14. Gallo J, Farbiarz J, Alvarez D. Análisis espectral de la variabilidad de la frecuencia cardíaca. Iatreia 12(2):61-71, 1999.
15. Goldberger A, Amaral L, Hausdorff JM, Ivanov P, Peng Ch, Stanley HE. Fractal dynamics in physiology: alterations with disease and aging. PNAS 99:2466-2472, 2002.
16. Rodríguez J, Prieto S, Correa C, Bernal P, Puerta G, Vitery S, et al. Theoretical generalization of normal and sick coronary arteries with fractal dimensions and the arterial intrinsic mathematical harmony. BMC Medical Physics 10:1-6, 2010.
17. Rodríguez J, Prieto S, Correa C, Bernal P, Álvarez L, Forero G, et al. Diagnóstico fractal del ventriculograma cardíaco izquierdo. Geometría fractal del ventriculograma durante la dinámica cardíaca. Rev Colomb Cardiol 19(1):18-24, 2012.
18. Goldberger AL, West BJ. Applications of nonlinear dynamics to clinical cardiology. Ann N Y Acad Sci 504:195, 1987.
19. Goldberger AL, Rigney DR, Mietus J, Antman EM, Greenwald S. Nonlinear dynamics in sudden cardiac death syndrome: heart rate oscillations and bifurcations. Experientia 44:983, 1988.
20. Pincus SM. Approximate entropy as a measure of system complexity. Proc Natl Acad Sci USA 88:2297, 1991.
21. Ksela J, Avbelj V, Kalisnik JM. Multifractality in heartbeat dynamics in patients undergoing beating-heart myocardial revascularization. Comput Biol Med 60:66-73, 2015.
22. Chang MC, Peng CK, Stanley HE. Emergence of dynamical complexity related to human heart rate variability. Phys Rev E Stat Nonlin Soft Matter Phys 90(6):062806, 2014.
23. Porta A, Bari V, Marchi A, De Maria B, Cysarz D, Van Leeuwen P, Takahashi AC, Catai AM, Gnecchi-Ruscone T. Complexity analyses show two distinct types of nonlinear dynamics in short heart period variability recordings. Front Physiol 6:71, 2015.
24. Rodríguez J. Nuevo diagnóstico físico y matemático de la monitoria fetal: predicción de aplicación clínica. Momento Revista de Física 44:49-65, 2012.
25. Rodríguez J, Prieto S, Ortiz L, Bautista A, Bernal P, Avilán N. Diagnóstico matemático de la monitoria fetal aplicando la ley de Zipf Mandelbrot. Rev Fac Med Univ Nac Colomb 54(2):96-107, 2006.
26. Rodríguez J. Entropía proporcional de los sistemas dinámicos cardíacos: Predicciones físicas y matemáticas de la dinámica cardíaca de aplicación clínica. Rev Colomb Cardiol 17:115-129, 2010.
27. Rodríguez J. Mathematical law of chaotic cardiac dynamic: Predictions of clinic application. J Med Med Sci 2(8):1050-1059, 2011.
28. Rodríguez J, Prieto S, Flórez M, Alarcón C, López R, Aguirre G, Morales L, Lima L, Méndez L. Physical-mathematical diagnosis of cardiac dynamic on neonatal sepsis: predictions of clinical application. J Med Med Sci 5(5):102-108, 2014.
29. Rodríguez J, Narváez R, Prieto S, Correa C, Bernal P, Aguirre G, Soracipa Y, Mora J. The mathematical law of chaotic dynamics applied to cardiac arrhythmias. J Med Med Sci 4(7):291-300, 2013.
30. Rodríguez J, Álvarez L, Tapia D, López F, Cardona M, Mora J, et al. Evaluación de la dinámica cardíaca de pacientes con arritmia con base en la teoría de la probabilidad. Medicina (Bogotá) 34(1):7-16, 2012.
31. Rodríguez J, Correa C, Melo M, Domínguez, D, Prieto S, Cardona DM, et al. Chaotic cardiac law: Developing predictions of clinical application. J Med Med Sci 4(2):79-84, 2013.
32. Rodríguez J, Prieto S, Domínguez D, Melo M, Mendoza F, Correa C, Soracipa Y, Pinilla L, Pardo J, Ramírez N. Mathematical-physical prediction of cardiac dynamics using the proportional entropy of dynamic systems. J Med Med Sci 4(8):370-381, 2013.
33. Rodríguez J, Prieto S, Bernal P, Izasa D, Salazar G, Correa C, Soracipa Y. Entropía proporcional aplicada a la evolución de la dinámica cardíaca. Predicciones de aplicación clínica. En: Rodríguez LG, coordinador. La emergencia de los enfoques de la complejidad en América Latina: implicancias políticas, epistemológicas y metodológicas para las ciencias del siglo XXI. Tomo 1,1a ed. Buenos Aires: Comunidad Editora Latinoamericana pp. 315-334, 2015.
34. Rodríguez J, Prieto S, Correa C, Mendoza F, Weisz G, Soracipa Y, Velásquez N, Pardo J, Martínez M, Barrios F. Physical mathematical evaluation of the cardiac dynamic applying the Zipf ? Mandelbrot law. Journal of Modern Physics 6:1881-1888, 2015. http://dx.doi.org/10.4236/jmp.2015.613193.
35. Rodríguez J, Correa C, Ortiz L, Prieto S, Bernal P, Ayala J. Evaluación matemática de la dinámica cardíaca con la teoría de la probabilidad. Rev Mex Cardiol 20(4):183-189, 2009.
36. Rodríguez J, Correa C, Prieto S, Bernal P, Forero G, Salazar G, Vitery S, Álvarez L, Puerta G. Confirmación del método de ayuda diagnóstica de la dinámica cardíaca de aplicación clínica desarrollado con base en la teoría de la probabilidad. Rev Fac Med 19(2):167-177, 2011.
37. Huikuri HV, Mäkikallio T, Peng CK et al. Fractal correlation properties of R ? R interval dynamics and mortality in patients with depressed left ventricular function after and acute myocardial infarction. Circulation 101:47-53, 2000.
38. Voss A, Schulz S, Schroeder R, Baumert M, Caminal P. Methods derived from nonlinear dynamics for analysing heart rate variability. Phil Trans R Soc A 367:277, 2009.
39. Rodríguez J. Comportamiento fractal del repertorio T específico contra el alérgeno Poa P9. Rev Fac Med Univ Nac Colomb 53:72-8, 2005.
40. Rodríguez J. Dynamical systems theory and Zipf-Mandelbrot Law applied to the development of a fetal monitoring diagnostic methodology. XVIII FIGO World Congress of Gynecology and Obstetrics. Kuala Lumpur, Malaysia. November 2006.
41. Borgatta L, Shrout PE, Divon MY. Reliability and reproducibility of nonstress test readings. Am J Obstet Gynecol 159(3):554-8, 1988.
42. Rodríguez J, Prieto S, Correa C, Pérez C, Mora J, Bravo J, Soracipa Y, Álvarez L. Predictions of CD4 lymphocytes count in HIV patients from complete blood count. BMC Medical Physics 13:3, 2013.
43. Rodríguez J, Bernal P, Prieto S, Correa C. Teoría de péptidos de alta unión de malaria al glóbulo rojo. Predicciones teóricas de nuevos péptidos de unión y mutaciones teóricas predictivas de aminoácidos críticos. Inmunología 29(1):7-19, 2010.
44. Rodríguez J. Método para la predicción de la dinámica temporal de la malaria en los municipios de Colombia. Rev Panam Salud Pública 27(3):211-218, 2010.
45. Rodríguez J, Prieto S, Correa C, et al. Theoretical generalization of normal and sick coronary arteries with fractal dimensions and the arterial intrinsic mathematical harmony. BMC Medical Physics 10:1-6, 2010.
46. Prieto S, Rodríguez J, Correa C, Soracipa Y. Diagnosis of cervical cells based on fractal and Euclidian geometrical measurements: intrinsic geometric cellular organization. BMC Medical Physics 14(2):1-9, 2014.